Paradigm

Backtracking

Backtracking can be applied only for problems which admit the concept of a "partial candidate solution" and a relatively quick test of whether it can possibly be completed to a valid solution.

When it is applicable, however, backtracking is often much faster than brute-force enumeration of all complete candidates, since it can eliminate many candidates with a single test.

It is convenient to implement this kind of processing by constructing a tree of choices being made, called the state-space tree. Its root represents an initial state before the search for a solution begins.

For backtracking, the tree is usually developed depth first.

• Resources

  • Addison-Wesley - Introduction to the Design and Analysis of Algorithms.3rd Edition.Oct.2011 - 12.1 Backtracking

Sorting

Bubble Sort

• Runtime: O(n^2) average and worst case
• Memory: O(1)
• i decides the element currently being sorted.
• Starting from the beginning will get a list sorted in ascending order.
• Starting from the end will get a list sorted in descending order.

Selection Sort

• Runtime: O(n^2) average and worst case
• Memory: O(1)
• Find the smallest element in the unsorted part and swap it with the first element of the unsorted part.

Insertion Sort

• Runtime: O(n^2) average and worst case
• Memory: O(1)
• Insert the marked element of each iteration into the partially sorted list.
• Shift sorted elements to make room
• In-place
• Stable

Shell Sort

• Determine the gap sequence is the key, use Knuth's sequence by default, as it's easy to generate: gap = (Math.pow(3, i) - 1) / 2 && gap < N / 3
• Unstable
• For each gap size, use gapped Insertion Sort

Merge Sort

• Runtime: O(nLogn) average and worst case

• Memory: O(n)

• Algorithm

  • Split the input in half recursively until cannot be further split
  • Merge the elements in sorted order and store them in the new space
  • Repeat this process with different input range until it covers the whole input

• Merge

  • The heart of the mergesort algorithm is the merging of two already-sorted arrays.
  • One extra array is needed to store the temporary and final result.

• Pros

  • O(nLogn)

• Cons

  • Extra space proportional to N
  • Slow for small input size
  • It goes through the whole process even if the array is sorted.

• Application

  • Useful for sorting linked lists in O(nLogn) time, as it doesn't require random access.

Radix Sort / Bucket Sort

• Challenges

  • How to store elements in buckets?

    • Use ArrayList or LinkedList to store elements in buckets.
    • Dutch National Flag problem (opens in a new tab) (3-way partitioning)

LSD Radix Sort

• Requires a stable sorting subroutine
• Suitable for fixed-length strings

MSD Radix Sort

Counting Sort

Pseudo code

• Assignment

  a := 1

• Use identation instead of braces

• Trace table for loop

  for i := 1 to 4
    x := i * i
  next i

  Variable / After each iteration	0 (Before loop starts)	1	2	3	4
  x		1	4	9	16
  i	1	2	3	4	5

Runtime Analysis

• Use -Xint to turn off JIT and AOT compilation and use interpretation only.

Dynamic Programming

• Deriving a recurrence relating a solution to the problem to solutions to its smaller subproblems.

Knapsack Problem

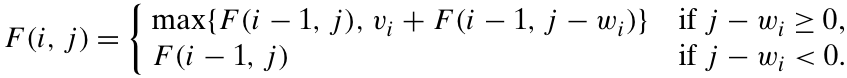
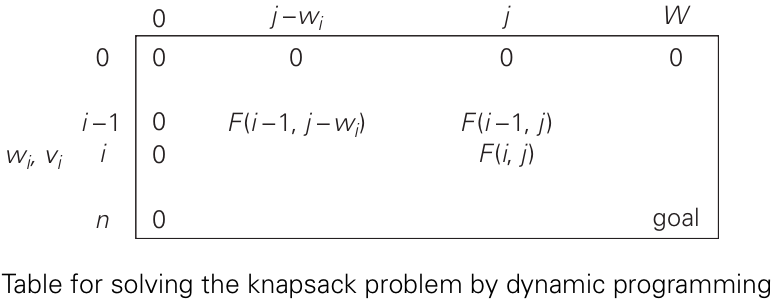
Implementation

Java

• Use System.arraycopy method for array shifting and moving.
• Use Arrays.copyOf method for array copying.